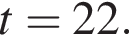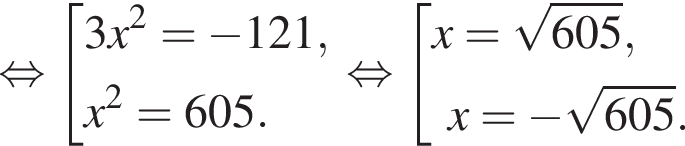Среди чисел 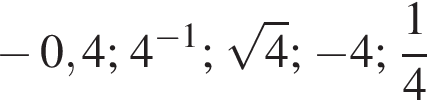 выберите число, противоположное числу 4.
выберите число, противоположное числу 4.
На клетчатой бумаге с клетками размером 1 см х 1 см изображён параллелограмм. Найдите его площадь в квадратных сантиметрах.
Если 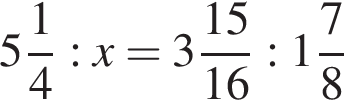 — верная пропорция, то число x равно:
— верная пропорция, то число x равно:
Результат разложения многочлена x (6a − b) + b − 6a на множители имеет вид:
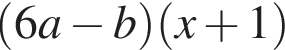
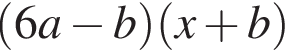
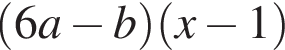
Одно число меньше другого на 64, что составляет 16% большего числа. Найдите меньшее число.
На рисунке изображены развернутый угол AOM и лучи OB и OC. Известно, что ∠AOC = 144°, ∠BOM = 136°. Найдите величину угла BOC.
Образующая конуса равна 14 и наклонена к плоскости основания под углом 60°. Найдите площадь боковой поверхности конуса.
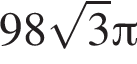
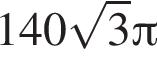
Расположите числа 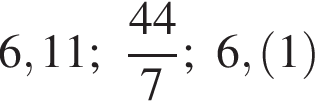 в порядке возрастания.
в порядке возрастания.
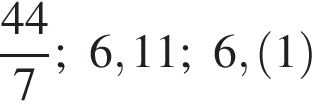
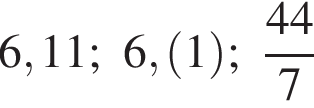
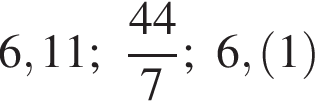
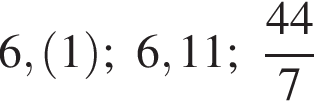
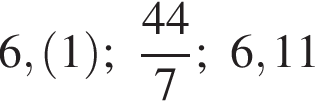
Выразите x из равенства 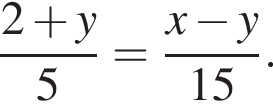
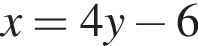
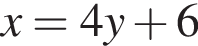


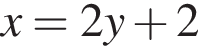
Прямая a пересекает плоскость α в точке A и образует с плоскостью угол 60°. Точка B лежит на прямой a, причем AB = ![]() Найдите расстояние от точки B до плоскости α.
Найдите расстояние от точки B до плоскости α.
Укажите область значений функции
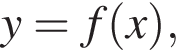 заданной графиком на промежутке [−2; 4] (см. рис.).
заданной графиком на промежутке [−2; 4] (см. рис.).
Свежие фрукты при сушке теряют a % своей массы. Укажите выражение, определяющее массу сухих фруктов (в килограммах), полученных из 60 кг свежих.
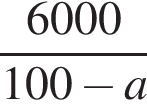
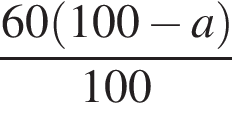
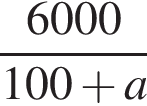
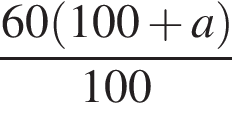
Прямая a, параллельная плоскости α, находится от нее на расстоянии 2. Через прямую a проведена плоскость β, пересекающая плоскость α по прямой b и образующая с ней угол 60°. Найдите площадь четырехугольника ABCD, если A и B — такие точки прямой a, что AB = 5, а C и D — такие точки прямой b, что CD = 3.
Упростите выражение
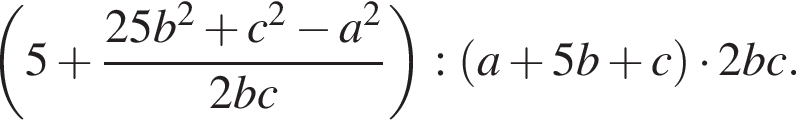
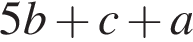
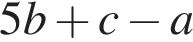
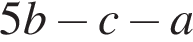
Корень уравнения 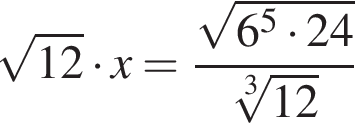 равен:
равен:
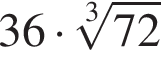
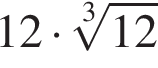
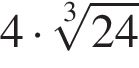
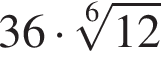
ABCDA1B1C1D1 — прямоугольный параллелепипед такой, что AB = 16, AD = 3. Через середины ребер AA1 и BB1 проведена плоскость (см.рис.), составляющая угол 60° с плоскостью основания ABCD. Найдите площадь сечения параллелепипеда этой плоскостью.
Сумма наибольшего и наименьшего значений функции
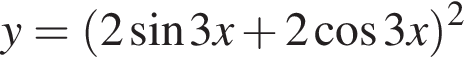
равна:
Корень уравнения
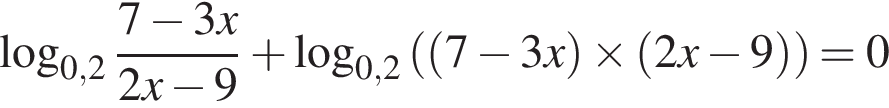
(или сумма корней, если их несколько) принадлежит промежутку:
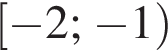
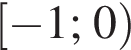
Витя купил в магазине некоторое количество тетрадей, заплатив за них 36 тысяч рублей. Затем он обнаружил, что в другом магазине тетрадь стоит на 1 тысячу рублей меньше, поэтому, заплатив такую же сумму, он мог бы купить на 3 тетради больше. Сколько тетрадей купил Витя?
Диагонали трапеции равны 15 и 36. Найдите площадь трапеции, если ее средняя линия равна 19,5.
Точки А(1;2), B(5;6) и C(8;6) — вершины трапеции ABCD (AD||BC). Найдите сумму координат точки D, если 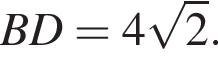
Пусть (x;y) — целочисленное решение системы уравнений
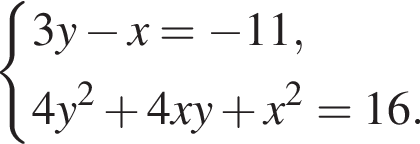
Найдите сумму x+y.
Найдите наибольшее целое решение неравенства 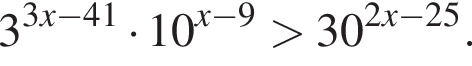
Найдите
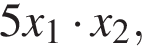 где
где ![]() — абсциссы точек пересечения параболы и горизонтальной прямой (см. рис.).
— абсциссы точек пересечения параболы и горизонтальной прямой (см. рис.).
Четырёхугольник ABCD вписан в окружность. Если 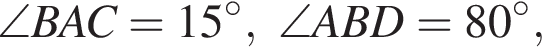 то градусная мера между прямыми AB и CD равна ...
то градусная мера между прямыми AB и CD равна ...
Найдите значение выражения: 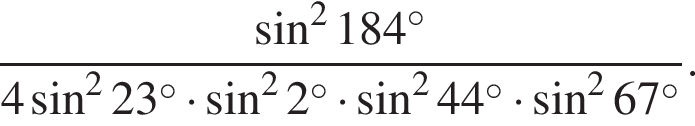
Найдите сумму целых значений x, принадлежащих области определения функции
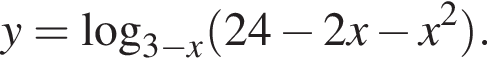
Прямоугольный треугольник с катетами, равными 1 и ![]() вращается вокруг оси, содержащей его гипотенузу. Найдите значение выражения
вращается вокруг оси, содержащей его гипотенузу. Найдите значение выражения ![]() где V — объём фигуры вращения.
где V — объём фигуры вращения.
Пусть 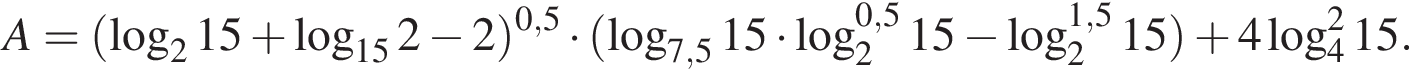
Найдите значение выражения 2A.
Найдите произведение корней уравнения 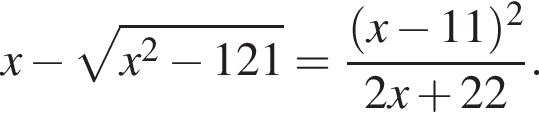

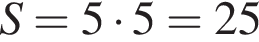 см2.
см2.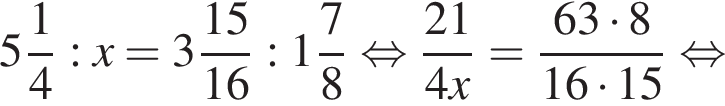
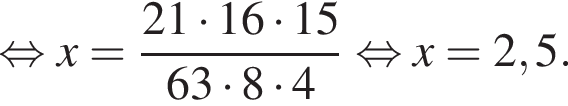
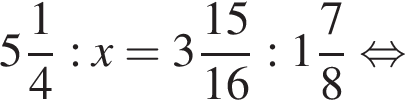
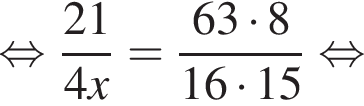

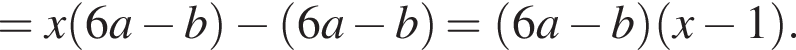

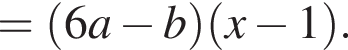
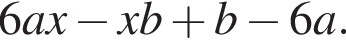
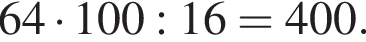 Таким образом, меньшее число
Таким образом, меньшее число 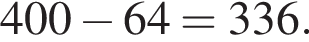
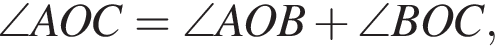
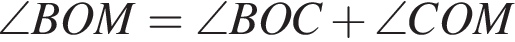 и
и  Таким образом:
Таким образом:
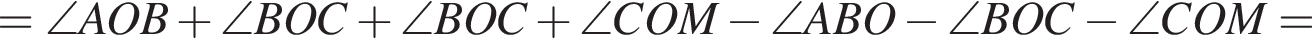
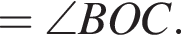

 где r — радиус основания, l — образующая. Найдем радиус:
где r — радиус основания, l — образующая. Найдем радиус: 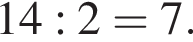 Таким образом, площадь боковой поверхности равна:
Таким образом, площадь боковой поверхности равна: 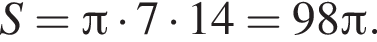
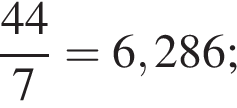


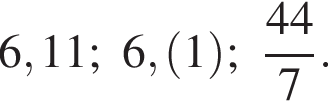
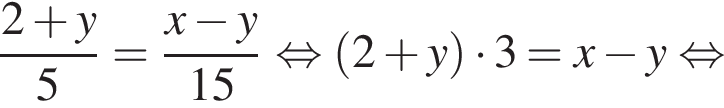
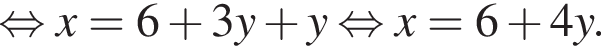
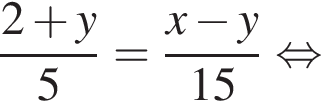
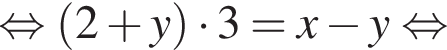



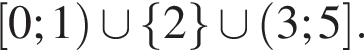
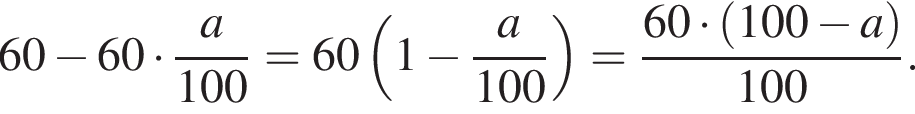
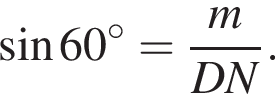
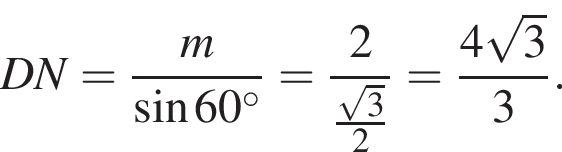
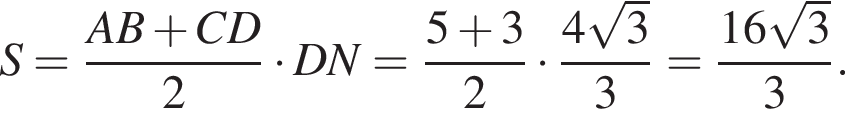
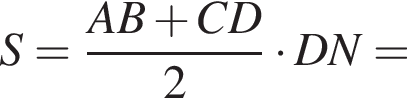
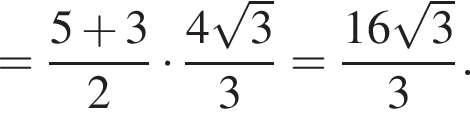
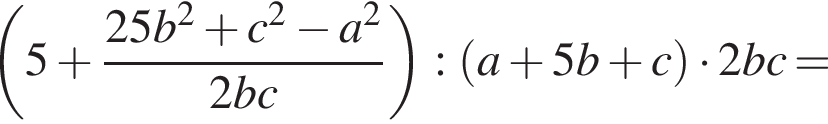
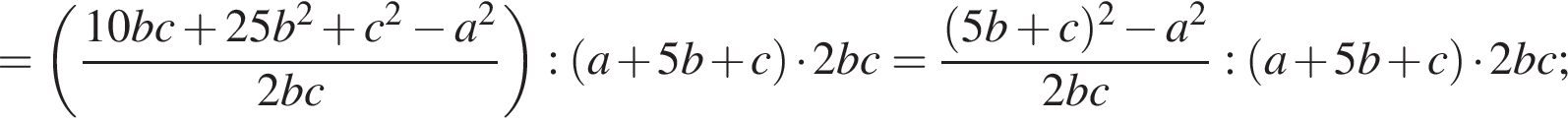
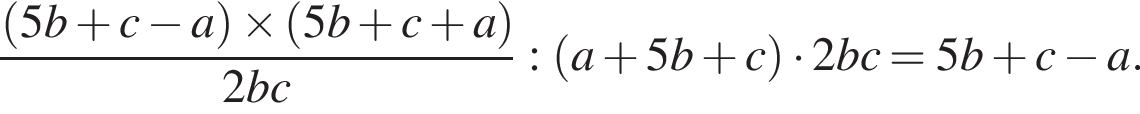
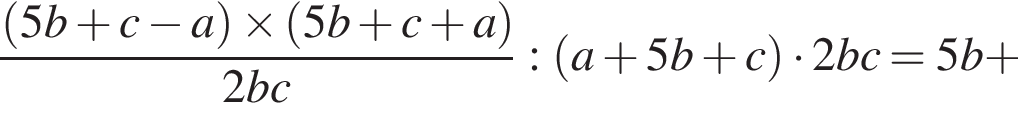
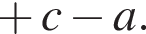
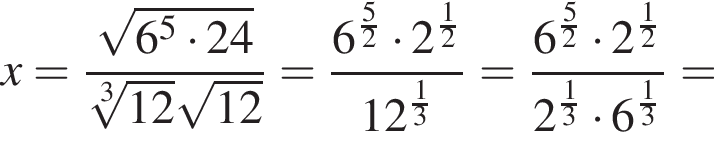
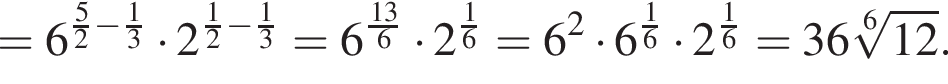
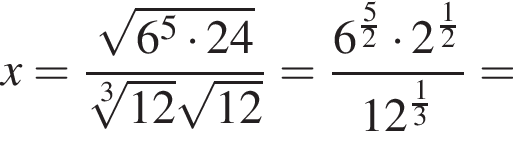
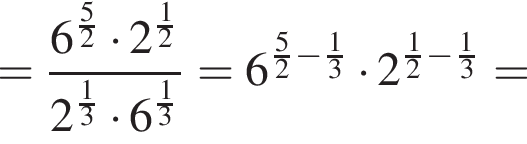
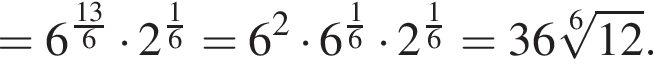
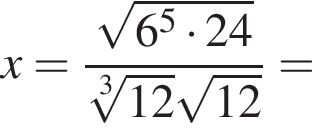
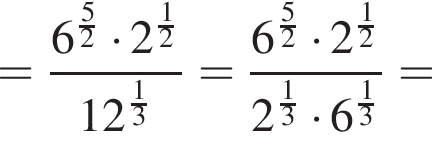
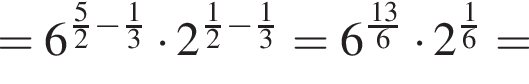
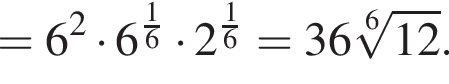

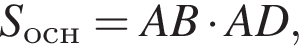 таким образом:
таким образом: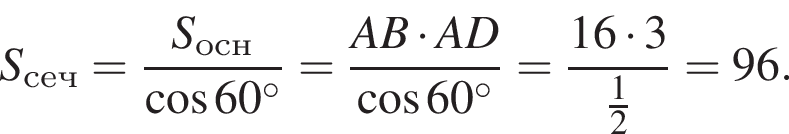
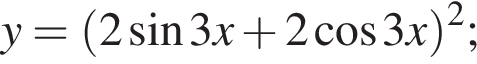


 имеем:
имеем:

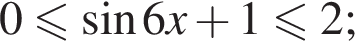
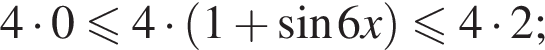
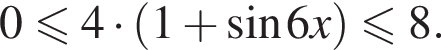
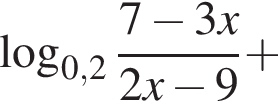

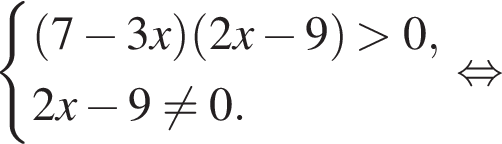
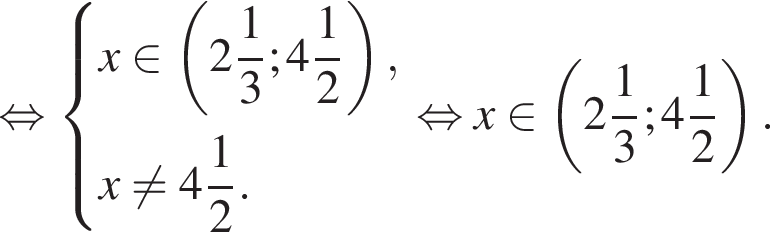
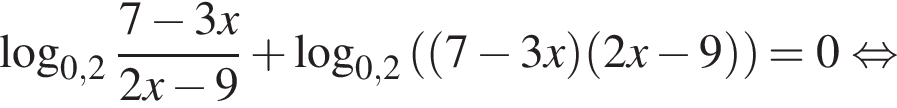
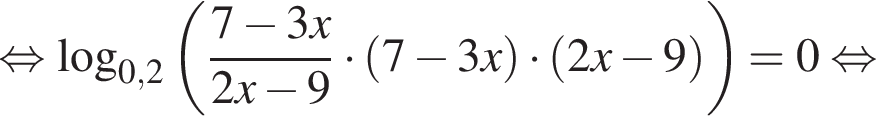
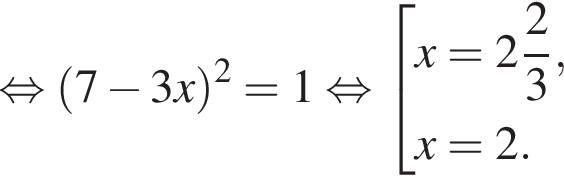
 Если бы Витя купил тетрадь в другом магазине, то было бы верно равенство
Если бы Витя купил тетрадь в другом магазине, то было бы верно равенство 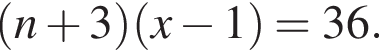 Решим систему уравнений:
Решим систему уравнений: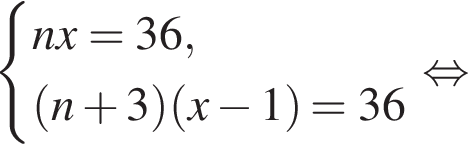
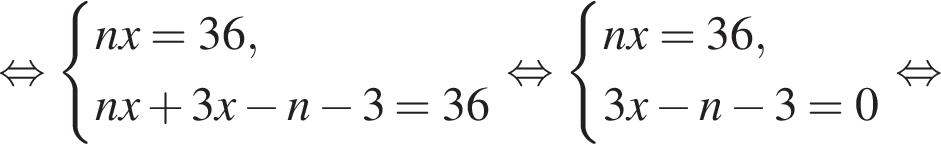
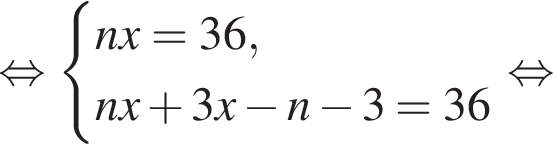
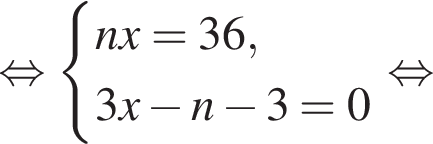
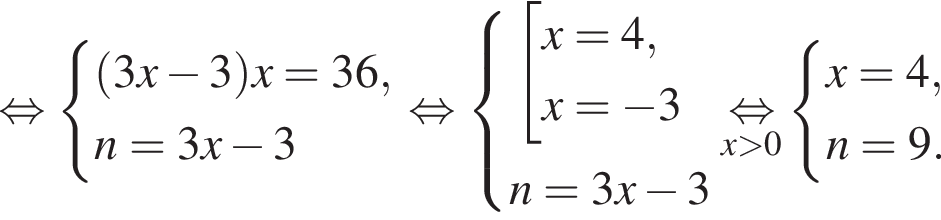
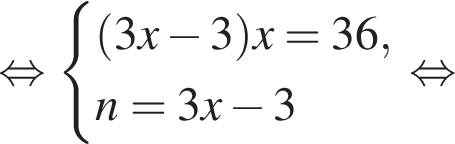
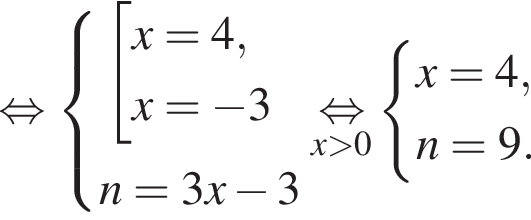
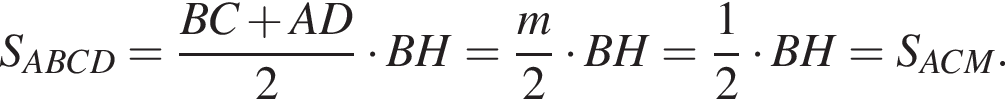
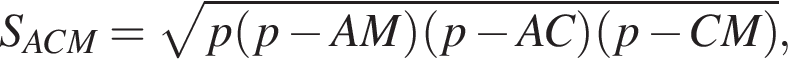 где p — полупериметр треугольника ACM, который равен:
где p — полупериметр треугольника ACM, который равен: 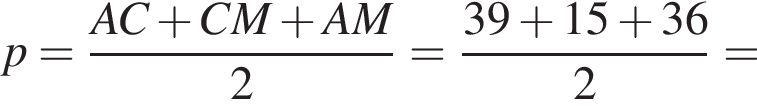

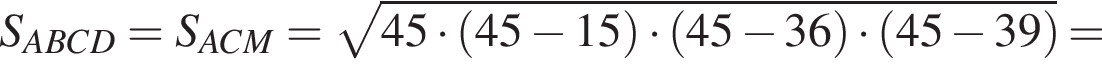
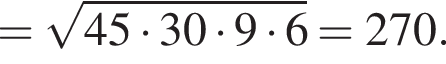
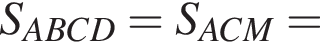

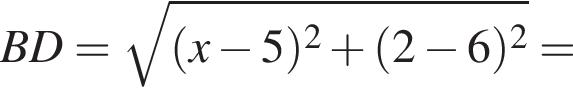
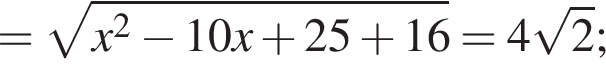
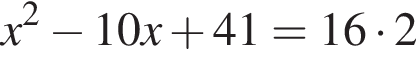
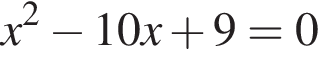
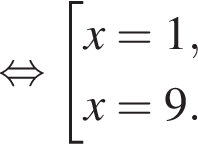
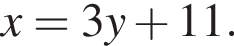 Заметим, что
Заметим, что  поэтому, подставляя x во второе уравнение системы получим:
поэтому, подставляя x во второе уравнение системы получим:
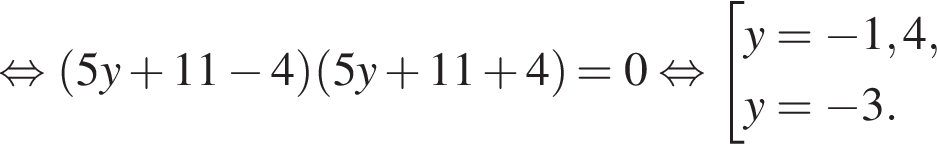

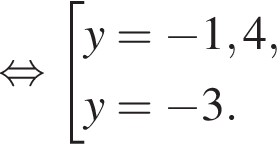
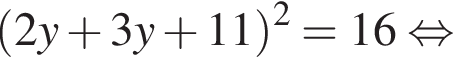
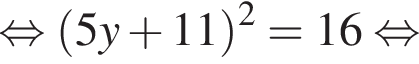
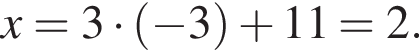 Сумма x+y равна:
Сумма x+y равна: 
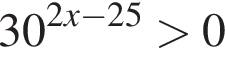 :
: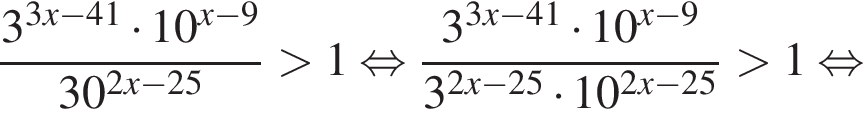
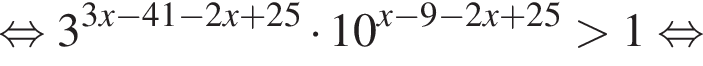
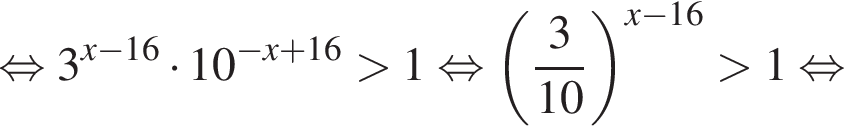
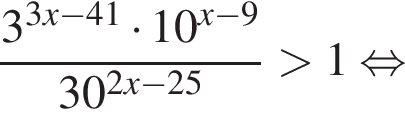
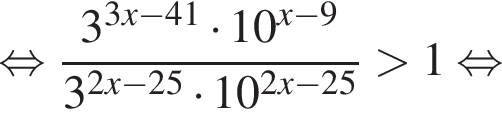
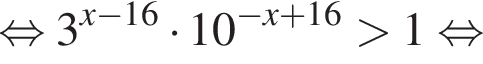
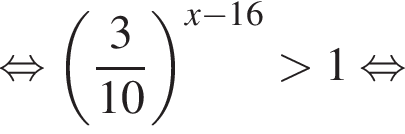
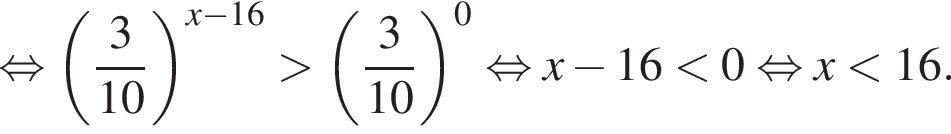
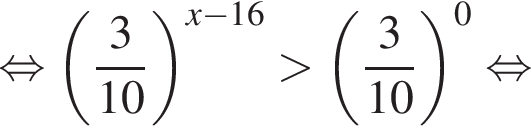
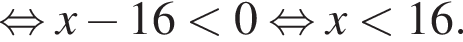
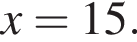
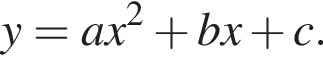 На рисунке изображена парабола с ветвями, направленными вниз, следовательно,
На рисунке изображена парабола с ветвями, направленными вниз, следовательно, 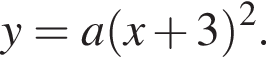 Для того, чтобы найти a, подставим в уравнение параболы точку (-2;-1), через которую данная парабола проходит:
Для того, чтобы найти a, подставим в уравнение параболы точку (-2;-1), через которую данная парабола проходит: 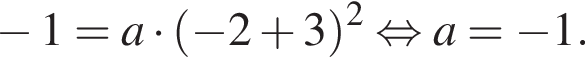 Таким образом, изображённая на графике парабола задается уравнением
Таким образом, изображённая на графике парабола задается уравнением 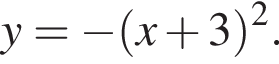
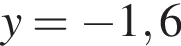 :
: 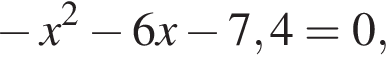 откуда по теореме Виета
откуда по теореме Виета 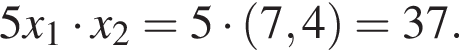


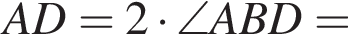


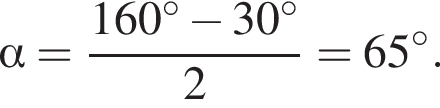
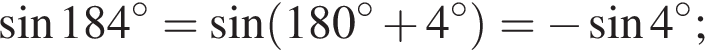

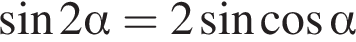 :
:
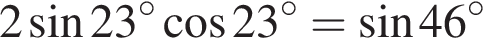
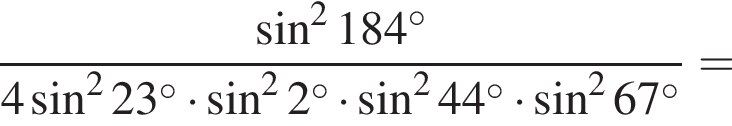
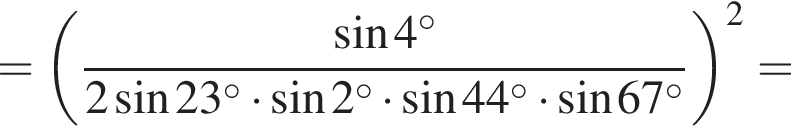
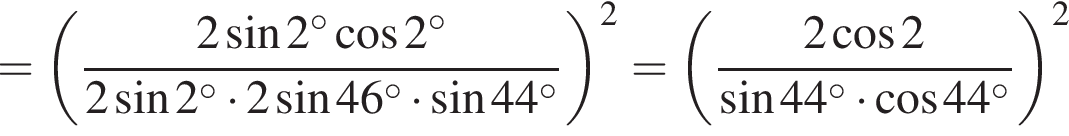
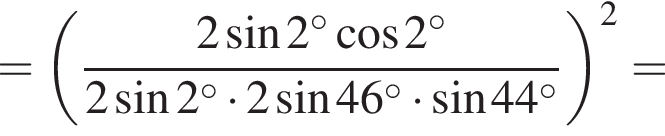
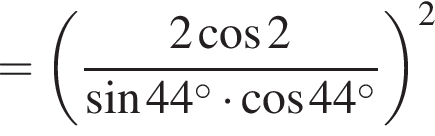
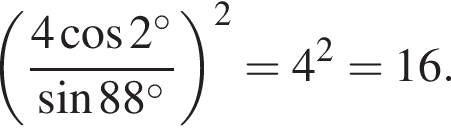
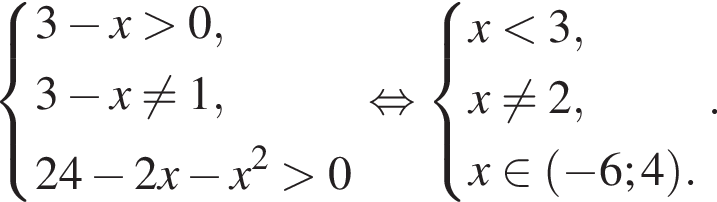
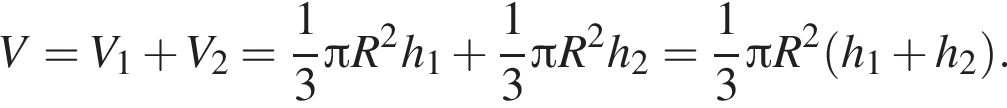
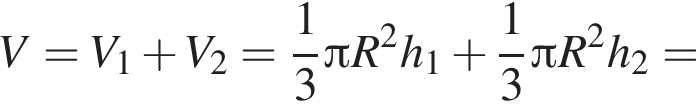
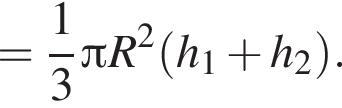
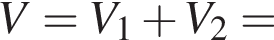
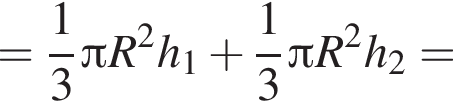
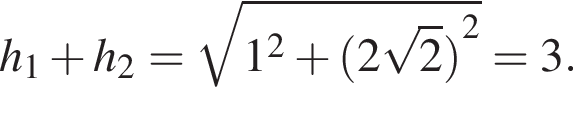
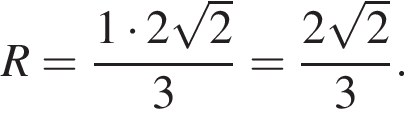
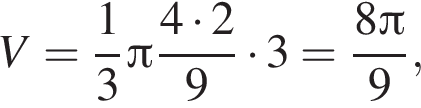 откуда
откуда 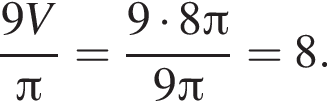

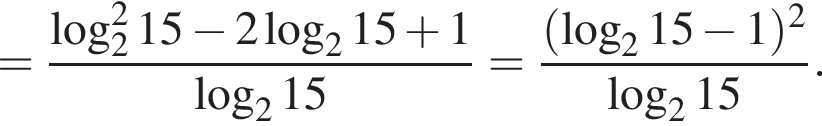
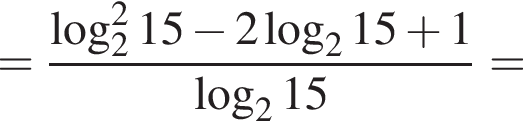
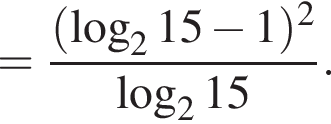
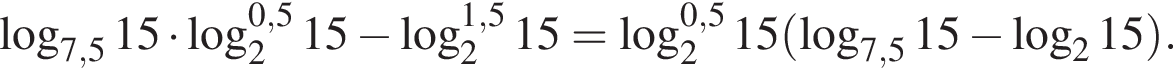
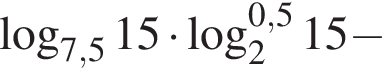
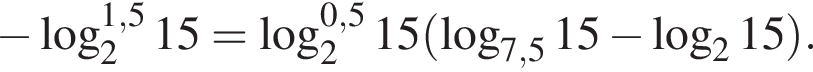
 Тогда имеем:
Тогда имеем: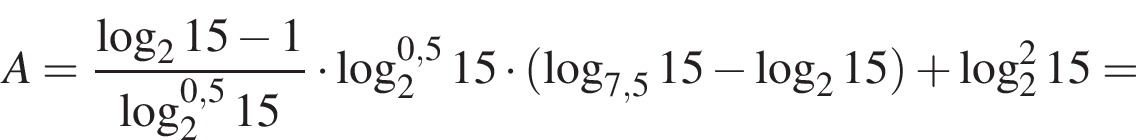
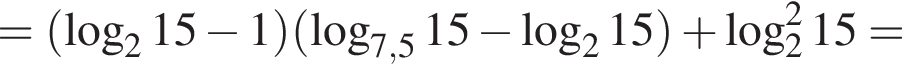
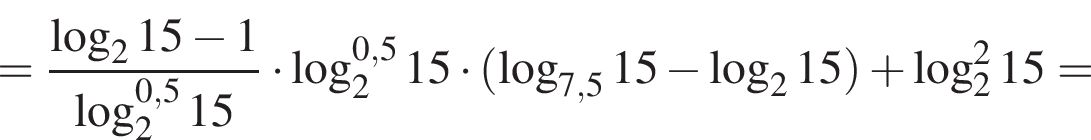
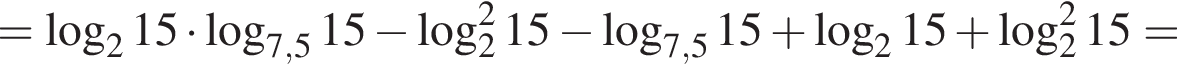
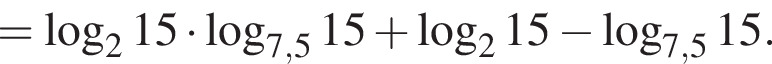
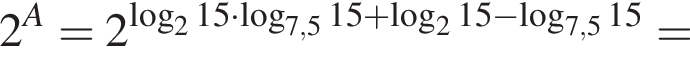
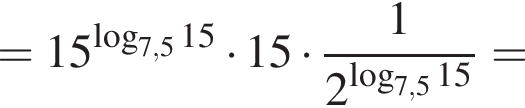
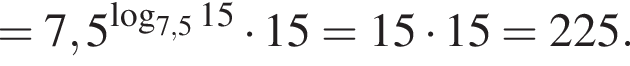
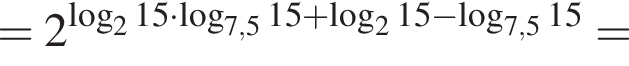
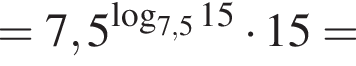
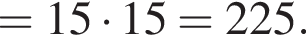
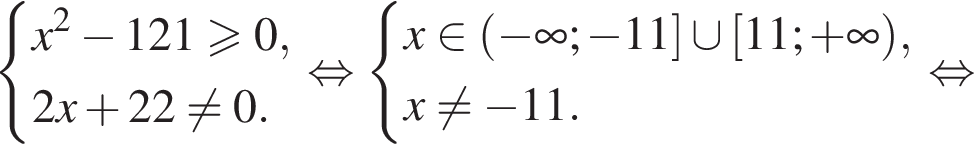
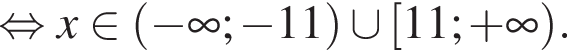
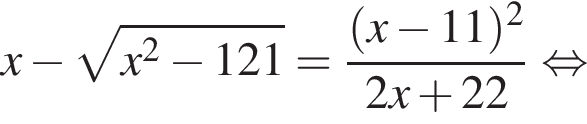
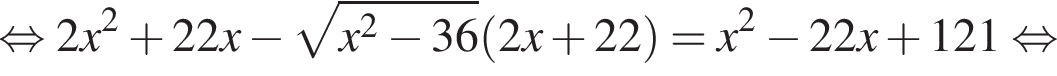
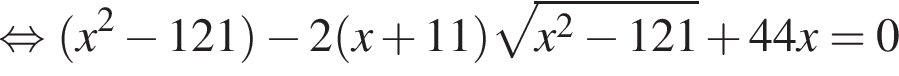
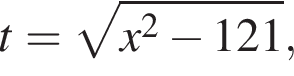 тогда
тогда 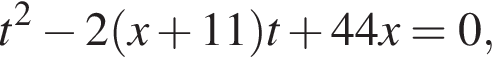 откуда
откуда 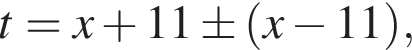 то есть
то есть